e start with a more general argument.  Let f(S,t) denote the value of any derivative security (e.g., a call option) at time t when the stock price is S.  Note that, by assumption,  the derivative price does not depend on the path of S, but only on the current value of S.

n the standard Black-Scholes option pricing analysis, the underlying asset pays zero dividends over the life of the option.  Here we consider relaxing this assumption to allow for the effects of a constant continuous dividend yield over the life of the option.

By Ito's lemma,

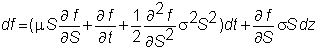
and recall that for the stock price

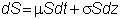
Now, consider the riskless hedge portfolio in Chapter 2, topic 2.4.

-k   derivative security

1    share of stock.

The number of derivative securities, k, is

 .

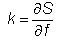
The value of this portfolio, V, is given by

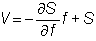
and the change in the value is

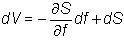
Substituting the df equation and the dS equation into this portfolio and rearranging, we get

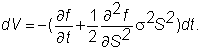
The important fact about this equation is that dV is independent of the stochastic term z.  This means that all the risk of the derivative can be hedged by holding

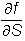
units of the derivative.

Since dV is instantaneously deterministic, the portfolio return must equal the instantaneous risk-free return.  In other words,

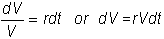
Substituting for dV and V, we get

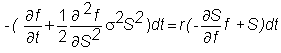
or

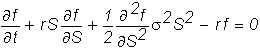
This is called the Black-Scholes (partial) differential equation.  The solution to this equation, subject to the appropriate boundary condition for f, determines the value of the derivative security.  For a European call option, the boundary condition is

f(S,T) = max{0,S-X}.

The solution of the differential equation for the call option is given by the Black-Scholes formula:

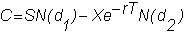
where

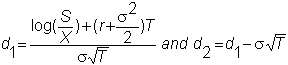
We can also apply Ito’s Lemma to derive the implied distribution of stock prices from a geometric Brownian motion model of stock prices.  The next topic Distribution of Stock Prices provides a technical overview of this issue.