D.2 Ito
Processes
|
|
e start by defining (standard) Brownian motion.
Our treatment is informal, and if you are interested in pursuing the
details and the derivations, we recommend you consult an advanced source such as
Duffie (1988).
A
stochastic process describes the evolution of a random variable
through time. Time can be modeled
discretely or continuously. Brownian
motion is a special continuous time
stochastic process that embodies the idea of "purely random" changes,
where the randomness is captured by the normal distribution.
Let
x denote the value taken by the process. For concreteness, think of x
as the price of the stock. At time t,
x can take on many values, depending
on the outcome of a random variable. This
randomness is modeled as follows.
Let
W be a set of states.
If state z occurs at time t,
then the value of x is x(t,z).
The randomness is described by a probability distribution on
W.
Brownian
motion is a special process that satisfies these assumptions:
1.
D(s,t)
= x(.,t) - x(.,s) is normally distributed for any t > s, with mean zero and variance (t - s) over the time interval
(t - s).
2.
If we take any n non-overlapping
intervals of time, then D(s1,t1),
D(s2,t2),...,D(sn,tn)
are all independent.
The
first property says that price changes are normally distributed while the second
property says that all price changes are independent.
The first assumption also says that the variance increases linearly with
time, and the expected price change is zero.
Brownian
motion comes very close to how we expect returns
to behave in an efficient market. Market
efficiency is the notion that the stock price embodies all available
information, and therefore price changes are unpredictable.
If price changes are normally distributed, then Brownian motion provides
a nice way to formalize this notion.
You
may find a "discrete time" analogue useful.
Think of the change in z, Dz,
in the period of time Dt,
as being described by
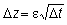
where
e is a normally distributed, random variable with mean zero and standard
deviation 1, and changes in z over two
non-overlapping intervals of time are independent.
Then,
E(Dz) = DtE(e) = 0
and
var(Dz) = (Dt)var(e) = Dt.
Brownian
motion is the limit of this process when Dt goes to
zero.
While
Brownian motion may be a nice model of returns, it is not quite as nice a model
of stock prices. Figure D.1 is
more what we want to capture.
Figure D.1
Stock Price as a Function of Time
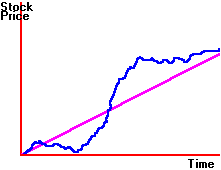
Here,
price changes are random, but have a positive drift.
This type of behavior is captured by a diffusion
process. A diffusion process in
its general form is written as
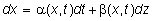
where
z is Brownian motion and a is
the drift term (which can depend on
both x and t). It controls the
deterministic growth rate of the process. b
is called the volatility term (and can also depend on both x and t).
The volatility controls how much the process is affected by the random
changes.
The
most common model of stock prices imposes a special structure on the drift and
volatility terms. This is the model
we have been using, and it is written as follows:
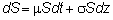
Here,
the drift and the volatility do not depend on time, but do depend on the stock
price. If you divide both sides by S,
you will get
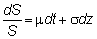
The
left-hand side is called the instantaneous
return, and it is made up of two factors.
The first is mdt,
which is the deterministic change in S. The second is due to the change in z, multiplied by a positive number, s.
The
number m
is called the drift rate of S and
s
is called the volatility.
This
is the equation that Black and Scholes use to model the behavior of a stock
price. It is often referred to as "geometric Brownian
motion." It says that S is expected to grow at rate m at
an instant of time, and the instantaneous return, dS/S, is normally distributed.
You
can see that if s =
0, the stock has zero volatility, and then
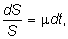
which
is the constant growth process when
there is no uncertainty.
The
price of a derivative security, such as an option or a futures contract, is
typically a function of time and the underlying stock price.
Generally, we can write this as a function f(x,t).
Of central importance is Ito's
Lemma (topic D.3), which allows the price dynamics for the derivative to be
derived. In addition, an application of this lemma allows both the Black-Scholes
Partial Differential Equation (topic D.4) and the Distribution
of Stock Prices ( topic D.6) to be derived.
 office (412)
9679367
office (412)
9679367