D.3 Ito's Lemma
|
H |
n this topic, we apply the theory developed in Topic 6.7 to an actual hedging example. Recall that initially, the arbitrage-free present value of the futures price is zero, but as subsequent shifts occur in interest rates, this is no longer the case. Here we consider the case of shifts in interest rates that occur subsequently to the time of settlement of the futures contract.
Here we assume that X is the price of some asset, and that price changes are described by the following general diffusion process:
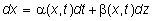
Let
f(x,t) be the value at time t
of any derivative security defined on x
(such as a call option). Here we
show that the derivative price, f,
also follows a diffusion process:
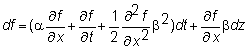
This
is an important characterization because it describes precisely how the common underlying source of uncertainty, dz, affects both asset and derivative prices.
Looking ahead, this enables a riskless hedge to be designed between the
asset and its derivative that eliminates dz, and the
value of the derivative to be derived from this hedge.
An
intuitive proof of the derivative price dynamics can be obtained by taking a
second-order Taylor's series expansion of f(x,t)
around a point (x0, y0).
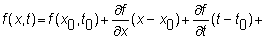
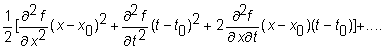
Now,
substitute
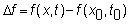
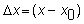
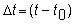
and
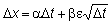
to
get
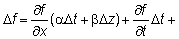
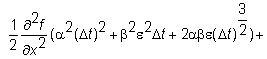
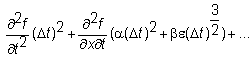
As
Dt approaches
dt, all terms involving (Dt)2
and (Dt)3/2
go to zero, as do any higher-order terms. The
critical part of the proof then shows that as Dt goes to
zero, the term b2e2Dt
becomes non-stochastic and converges to b2dt. To see
that the Dt term does
not go to zero, we can write the discrete time analogue of Dx
as
.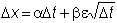
Therefore, (Dx)2
retains Dt, which approaches dt
as Dt goes to zero.
With
this, the formula simplifies to
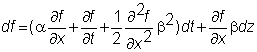
which
is known as Ito's Lemma. It says that if
f is a function of x and t, then f
inherits the stochastic properties of x,
and the drift rate and volatility have to be adjusted as given by the lemma.
In particular, df is also
normally distributed.
For
the stock price, we have
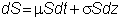
Substituting
for x, a and b in the df
equation yields:
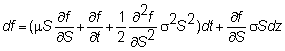
This
is the general expression for the change in a derivative's price given the stock
price process.
In
the next topic, we apply Ito's Lemma to derive the Black-Scholes
Partial Differential Equation. This
equation expresses the relationship between the “unknown” option valuation
function and some of its partial derivatives.
 office (412)
9679367
office (412)
9679367