6.5
Interpretation of the Black-Scholes Model
|
|
t first glance, the Black-Scholes formula for the value of a call option seems
complex:

where
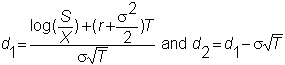
and
N() is the cumulative standard normal distribution.
You
can see that the option's value depends on five variables:
the stock price, the risk-free interest rate, the stock's volatility, the
strike price, and time. In Chapter
7, Hedge Parameters and Comparative Statics,
we discuss how the option price varies with these parameters.
Online, you can get an understanding of this dependence in Option Tutor's
Option Sensitivities subject.
If you are in this subject online select the option price for the Y-axis,
and then systematically select the five variables for the X-axis.
Notice
that the option price does not depend on the expected return from the
option (or from the stock). In
a conventional asset pricing model such as CAPM, you may recall that typically
we value risky assets by discounting future cash flows by a risk-adjusted
discount rate. The appropriate
discount rate depends on risk attitudes of investors.
These attitudes determine the "market price of risk," which is
the rate at which you can trade risk for return.
In
the Black-Scholes model, however, these considerations play no role.
The reason has to do with the riskless hedge argument. In constructing the riskless hedge, what you are doing is
diversifying all the risk from the option using the stock.
In a precise sense, then, the option does not introduce any additional
risk that must be priced in the market. Similarly,
the option does not permit any additional risk to be diversified away by
investors. Instead options permit a transfer of risk from buyer
to seller.
Another
way to see this is to return to the binomial model, where we use the stock and
the bond to create a synthetic option.
That argument shows you that the option is a redundant security,
and therefore determining its price cannot involve any additional considerations
of risk. All the risk that must be
priced has already been accounted for in the stock price. From this approach you can also see that the option contract
allows the transfer of but not the reduction of risk. In addition, because you can create a synthetic option from a
stock and a bond, and the prices of these securities are observable, it should
be clear that in principle the option value can be determined using these prices
and arbitrage arguments.
Of
course, these arguments all depend on knowing how to construct the riskless
hedge. Both the binomial and
geometric Brownian motion assumptions allow us to construct the riskless hedge.
This would not be the case, for example, if the stock followed a
trinomial process (as you saw in Chapter 4, topic 4.2's discussion of The
Economics of Retrading). In that case, the option value cannot be determined by
arbitrage arguments alone, and risk attitudes would again enter the picture.
An
immense advantage of the Black-Scholes model is that it provides a closed-form
solution for the option price. This
means that, given the parameters required by the model, we can solve for the
option value almost instantaneously. Chapter
13 lets you work through an application of this model to a real world option
valuation problem.
The
model also tells us how sensitive the option price is to the parameters. This is useful in managing the risk of an option position,
which is the subject of Chapter 7, Hedge
Parameters and Comparative Statics.
 office (412)
9679367
office (412)
9679367