How would you value a call option in a world with certainty, where stock prices exhibit constant continuous growth?

The answer to this question provides a useful introduction to the option valuation problem in a world with uncertainty.  To start answering the question, we will need to introduce some notation.

Notation

X    = strike price of the option;

T    = expiration date of the option;

S    = current market price of the stock;

ST  = price of the stock when the option expires; and

r     = risk-free interest rate

Continuous Time

The return on a stock between periods t and t+1   is given by

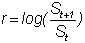
This is the "continuously compounded" return, which means that if the stock grew continuously between periods t and t+1 at rate m, then St would grow to St+1.  In other words,

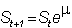
If m is constant over time, then we know the value of the stock price at the time of the option's expiration, T .

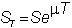
or, equivalently, the current stock price is the present value of the stock price at the time of the option's expiration:

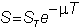
Certainty Option Pricing Model

In our world, since the stock price at time T is known, the terminal value of the option is also known.  From the definition of a call option, the call is exercised only if it finishes in-the-money (i.e., the stock price at time T   exceeds the strike price).  Thus, it is either worth zero (and left unexercised), or it is in-the-money and worth the difference between the stock price at time T and the strike price.  Mathematically, this value is expressed as:

Call Value = max {0, ST - X}

Since there is no uncertainty, we can find the current value of the call option: it is simply the terminal value discounted back to today at the risk-free interest rate:

Current Call Price =  PV( max {0, ST - X} )

And, with continuous compounding at r, the present value is:

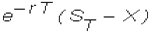
If the call option has zero value at time T, then the call option has zero value at any other time. If the call finishes in-the-money, then the current value is

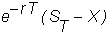
We know that if the growth rate of the stock is r, then S is the present value of the stock price at time T.  But if there is no uncertainty, and r   is the risk-free interest rate, then S must grow at rate r.  Otherwise, there is an arbitrage opportunity (if, for example, S grows at a smaller rate, you should sell the stock and invest the proceeds in the bond).

Therefore, if the call finishes in-the-money, its value is

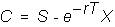
This price has an easy interpretation.  It equals the stock price minus the present value of the exercise price. 

In Chapter 5, topic 5.2, Binomial Option Pricing: N-Periods, you saw that this equation has the same structure as the binomial model.  The major difference is that in the binomial model, the first and second terms are weighted by probabilities, to allow for uncertainty.

Application of the Certainty Model

So how well does the certainty model perform?  Consider the following data for call options trading on IBM, the price information taken from FAST trading room at Carnegie Mellon University on Friday, October 15,1993, at 14:55:43 (i.e., 2:55). 

Last traded price for IBM:  44 1/2

Current bid price for IBM:  44 3/8

Current ask price for IBM: 44 5/8

Yield to maturity for a Treasury Bill with approximately the same life as the option: 2.867%.

Ex-dividend date for IBM: 11/5

Dividend payment date: 12/10

Estimated IBM dividend during life of option:  $0.25

Continuously compounded yield to maturity for a t-bill maturing around this dividend payment date: 2.922%.

Maturity date for November 1993 options: November 20.

Option information from the CBOE for the November options at this same time is presented in Table 6.1.

Table 6.1

Chicago Board of Exchange Data 

We will now apply the certainty model to this data.

The first problem is that IBM will pay a dividend after the option's expiration date, but the stock goes ex-dividend prior to the November expiration date.   This affects the stock price during the life of the option because the stock price will fall by the amount of the dividend on the ex-dividend date.

To accommodate this problem, we will adjust the current stock price by subtracting the present value of the dividend payment D.  The option holder is only concerned with the stock after the ex-dividend date.  Therefore,

= 0.25 x exp(-.02922*58/365)

= 0.2488

The present values of the strike prices are computed in Table 6.2.

Table 6.2

Present Values of Strike Prices 

The certainty option pricing model is applicable by adjusting for the dividend.  That is:

Certainty Value: Max (0, S - PV(Dividend)  - PV(X))

Substituting the numbers, we get the following values for the November call options, compared with the bid/ask spread in the options market:

Table 6.3

Call Options

You can see that the certainty model has systematically underpriced the options.

Why is this the case?  There are at least two factors we have missed.  First, these are American options, and there may be some value to early exercise.  Second,  the stock price at the terminal date is not known.  This uncertainty raises the value of the option. 

To see why, consider a simple example.  Suppose the  price of a non-dividend-paying stock at time T equals the present value of the strike price X.  In the certainty model, the call has zero value.  Now, suppose the terminal stock price is either increased by some small positive number, e, or decreased by e with equal probability.  The expected terminal stock price is the same, but the call has positive value, because in the "plus" event, you get:

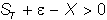
while in the "minus" event, you still get zero.  In fact, if you make e larger (i.e., increase the volatility), the call will increase in value.  Intuitively, what is happening is that as  volatility increases, there is a greater chance that the call will be deeper in-the-money.

As a result, you should be able to do better than the certainty model in the presence of volatility.   You can read this in the next topic Stock Price Dynamics.