rom the Lemma the excess drift rate divided by the volatility is equal for the stock and the call option.  This means that again we merely have to simplify the equation

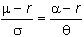
The two assets are the call option and SBd, the value of the deliverable bond in the strike currency.  The price of the call option is always in units of the strike currency (k); the exchange rate is the number of units of the deliverable currency in units of the strike currency.

The exchange rate process is

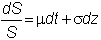
The call option, C, is assumed to be a function of S and t.  Ito's lemma  implies that the drift rate of the call option is:

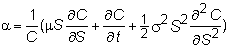
and the volatility is

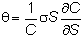
The second asset is SBd.  Bd grows at rate rd  where d denotes units of deliverable currency:

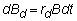
Totally differentiating SBd, we get d(SBd) = S(dBd) + (dS)Bd.  Substituting for dS and dBd, we find that                                                                                                                               

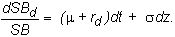
The general method for valuing options then implies that

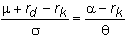
If we substitute for a and q and simplify, we get the partial differential equation for the currency call option:

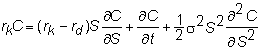
This equation differs from the original Black-Scholes equation by only the continuous zero-coupon bond yield. The continuous dividend yield PDE is reproduced for your convenience as:

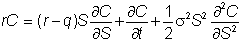
You can see that the solution to the currency option PDE must be the same as the continuous dividend yield case when rd is substituted for the constant continuous dividend yield term q, and rk is substituted for r.

In the next topic, Application:  Options on Futures, we apply the same technique to derive Black's Model for options on futures.