12.2
Application: Stock Options
|
|
ere, we show you how this lemma lets us derive the basic Black-Scholes partial
differential equation. For convenience, we restate Ito’s lemma applied to the
call option:
Ito’s
Lemma: If dS = mSdt + sSdz,
and C(S,t) is the price of the call option, then
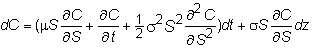
You
should note that the drift rate of the call is (1/C) times the term multiplying dt:
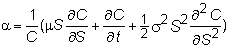
and
the volatility is (1/C) times the term
multiplying dz:
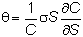
Stock
Options
Let
S be the stock and C
the call option on the stock. The
lemma says that the excess drift rate divided by the volatility should be equal
for the stock and the call option. This
means that for a non-dividend paying
stock:
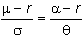
All you have to do is
substitute for a and q and simplify to construct the Black-Scholes PDE (see
the next topic Construction of the Black-Scholes).
This is:
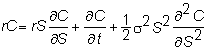
![]()
Finally,
the required adjustment for options defined on an asset that pays a continuous
constant dividend requires that the equation be defined as:
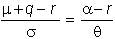
 office (412)
9679367
office (412)
9679367