rom the Lemma the excess drift rate divided by the volatility is equal for the future and the call option.  This means that again we merely have to simplify the equation

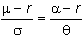
We start with the assumed futures price process:

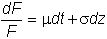
Assume that the value of the call option is C(F,t), and applying Ito’s lemma to C,

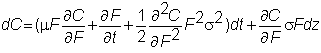
Recall that the drift rate of the call is (1/C) times the term multiplying dt, and therefore the drift rate of C is

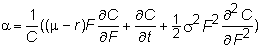
and the volatility is

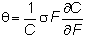
Following the general method for valuing options, we can equalize the volatility-adjusted drift rate on the stock and on the call option:

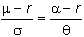
Substituting for a and q, we get

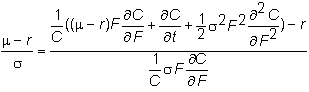
Now, cancel the s in both denominators, multiply the right hand side through by C,  and multiply out the denominators to get

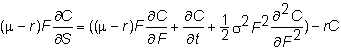
Finally, cancel the (m-r) term on either side to get

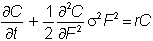
The solution to this equation is Black’s model.

In Chapter 13, Valuation Examples and Techniques, you will see how option pricing theory is applied to real world problems.