et S be the stock, and C the call option on the stock.  From the Lemma the excess drift rate divided by the volatility is equal for the stock and the call option.  This means that we have to simplify the equation

where

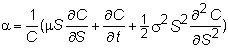
and

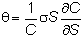
Substituting for a and q, we get

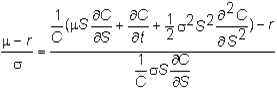
We now take the following steps:

1.  Cancel the s in each denominator:

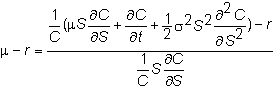
2.  Multiply the numerator and denominator of the right-hand side by C:

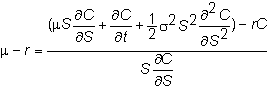
3.  Multiply each side by the remaining denominator:

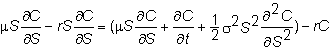
4.  Cancel the term

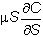
  on each side:

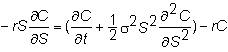
5.  Re-arrange to get

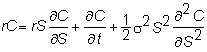
This is the usual form of the Black-Scholes partial differential equation.

If the stock pays a continuous dividend yield, q, then the two volatility-adjusted drifts are still equal.  This equality, however, is adjusted to account for the continuous dividend yield (q) received by a stockholder:

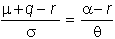
Thus, by repeating the above steps,  an additional term is created:

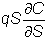
and the PDE is

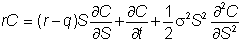
A widely used application of the continuous dividend yield model is the option pricing model for currencies. Details of how the general method applies to currencies are presented in the  next topic Application: Currency Options.