n the two-period case, we can write the call option value with respect to risk-neutral probabilities  p as:

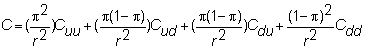
This two-period form can be rearranged into a form that allows the general structure to be deduced.

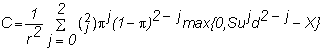
Written in this form, the general formula for n-periods is

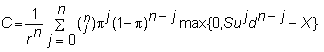
That is, we are summing over the 2n possible paths that the underlying stock price can take.  Note, however, that because u, d, and r are constants, the option pricing problem is not path-dependent.

In this case, a path can be defined in terms of some number of realized upticks and some number of realized downticks that sum to n.  With this observation, let m be the smallest number of upticks for which a path is in-the-money.  We can ignore any path with less than m upticks because the call option will finish out-of-the-money.

Thus, if we let m be the smallest integer such that Sumdn-m > X, then we can simplify the general formula by eliminating all stock paths with fewer than m upticks:

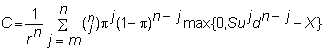
Since we know that the option will finish in-the-money on all these paths, we no longer need to take the max, and so we get:

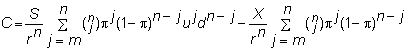
This expression still has the simple form of the two-period model.   The second term is the (risk-neutral) probability that the call option will be in-the-money multiplied by the exercise price, all discounted by the risk-free rate.  Therefore, it is the discounted value of the expected payment.

The first term is the discounted value of the expected revenue.  Unlike the expected payment, the expected revenue is not equal to S times the probability of the call being in-the-money, because the revenue depends on the stock price (while the payment does not).  Rather, we calculate the expected revenue, as done in the formula.

Using the definition of p, this can be rewritten as

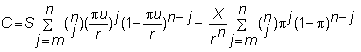
Let  q =  pu/r.  Then, using the binomial distribution notation, the present value of the call option equals

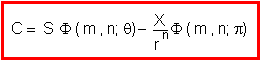
Next, we consider the limiting behavior of this pricing model as n gets larger.  This is described in topic 5.4,  Binomial Option Pricing:  Limiting Results, and formally derived in the technical appendix to this chapter.