3.4
American Put Option: Zero-Dividend
Case
|
Y |
ou
have found that an American call option should not be exercised prior to
maturity. What is the case for the American put option?
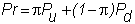
where p
is the risk-neutral probability (see topic 2.7, Risk-Neutral
Valuation Principle in Chapter 2), and r
is one plus the interest rate. In
the one-period model Pu
and Pd are the terminal put
option values. In other words, Pu
= max{X-Su,0} and Pd
= max{X-Sd,0}.
Substituting
these values, we get:
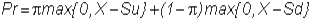
and
adding and subtracting X in the
right-hand side of the equation yields:
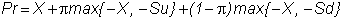
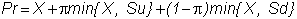
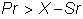
which
implies P > X/r - S since r >
1.
But
what is the put option worth if you exercise it?
If
you exercise the put option, you sell a stock worth S
and receive the strike price, X.
The exercise value is thus X - S,
and since r > 1 it is possible that the exercise value of the put option is
greater than the value if you hold onto it:
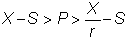
This
is so when S is very close to zero, so P
is approximately X/r, and thus early
exercise is always desirable since r
> 1.
Therefore,
the right to early exercise may have value for an American put option.
Unfortunately,
there is no formula that gives you the price of an American put option. Various numerical methods have been developed to calculate
its value. One such method is based
on the binomial model, where you check at every node whether the option should
be exercised.
Another
variable which affects the decision to exercise an option early is the dividend
paid by the stock. We deal with
this next in the topic Dividends
and American Options.
 office (412)
967-9367
office (412)
967-9367