3.6
Two-Period European versus American Option Example
|
I |
n
this topic, we start by working through a two-period European option pricing
problem, and then compare it with American options.
We use the risk-neutral valuation principle since it provides a
straightforward method for computing the values for both types of options.
Assume
the following:
S = $10
u = 2
d = .5
r = 1.01 per
month
X = 15
1-period
= 1 month
Here,
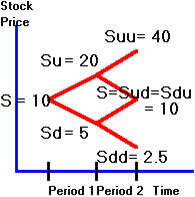
the initial stock price of 10 can double or halve every period.
Using the tree representation, we get the results shown in Figure 3.7.
Figure 3.7
Tree Representation for Stock
European
option values defined on this tree can be computed in a straightforward manner
by using the risk-neutral probabilities. Recall
that these probabilities are:
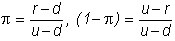
respectively,
for an uptick and a downtick. In
this example, these equal 0.34, and 0.66, respectively.
European
Call Option Values
The
value of a European call option at the uptick node is obtained from the formula:
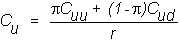
where
Cuu and Cud
are the terminal values of the call option (i.e., the values of the call at the
two nodes after the first uptick). A
similar procedure is applied at the downtick node, and finally repeated at the
initial node. The call option tree is depicted in Figure 3.8.
Figure 3.8
Tree Representation for Call Option
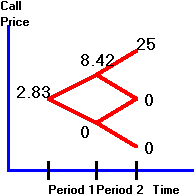
Here,
Cuu = 25 = Suu
- X = 40 - 15.
American
Call Option Values
You
have seen (topic 3.3, American Call Option: Zero-Dividend Case) that if there are no dividends, a
call option should not be exercised early.
Since the stock in this example does not pay any dividends, this means
that the American option should be worth exactly the same as the European one.
You
can verify this using this same example. In
the tree, shown in Figure 3.9, there are two values depicted at each node. The bottom value is what you get if you exercise the call,
and the top value is what you get if you do not exercise the call.
Figure 3.9
Call Value: Exercised versus
Unexercised
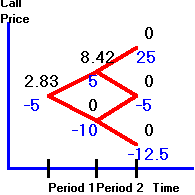
Clearly,
you would not choose to exercise at any node, except where there are two upticks.
European
Put Option Value
You
can compute the European put values, strike = 15, at each node either from the
risk-neutral valuation principle or from put-call parity.
The tree diagram for put values is shown in Figure 3.10.
Figure 3.10
European Put Option Values
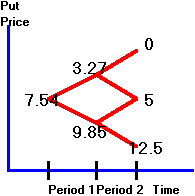
American
Put Option Value
Recall
(see topic 3.4, American Put Option: Zero-Dividend Case) that even without dividends, there
may be value in early exercise of an American put option.
As a result, you have to check for this possibility at every node.
The
tree in Figure 3.11 displays two values at each middle node and three values at
the first node. The top number is
the (European) value of the unexercised put option, and the bottom
(middle) number is the value of the put option exercised.
The bottom number at the first node is the American put value and online
it appears in red:
Figure 3.11
American Put Option Value
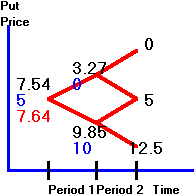
You
can see that if a downtick occurs in period 1, the stock price equals 5 and the
exercised value of the put option is 15 - 5 = 10.
The unexercised value is the
same as the European put option value of 9.85.
As a result, the risk-neutral price at time 0 is now:
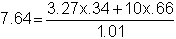
In
the next topic Two-Period Asian Option Example
you can see how to apply the binomial model to the problem of valuing a non-standard
option.
 office (412)
967-9367
office (412)
967-9367