2.5 PUT OPTION VALUATION:  A RISKLESS HEDGE APPROACH

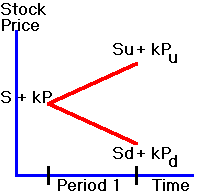
Consider a portfolio of +1 stock and +k puts.  The future payoffs for this portfolio are shown in Figure 2.5.

Figure 2.5

Future Payoffs

The Hedge Ratio (k)

For a portfolio to be riskless, you have to choose k so that the payoff in both states is equal, whether the stock moves up or down.

This requires

which is called the hedge ratio.

The Riskless Hedged Portfolio:  Put Options

The portfolio in Figure 2.5 is known as the riskless hedged portfolio.  It is constructed from the hedge ratio k, so that for every stock held long k put options are bought.  The riskless (put option) portfolio is:

S  + kP

This is a riskless hedge because when the terminal stock value is low, the put is valuable.  The converse is true for a high terminal value.  Setting k equal to the hedge ratio balances the losses with the gains.

The Cost of the Riskless Hedge

The cost of acquiring this portfolio today is S + kP.  Since

the portfolio end-of-period payoff is a certain amount.  Thus, using the risk-free interest rate, you can equate the cost of acquisition today to the present value of the certain end-of-period payoff.  The end-of-period payoff can be defined by either the up- or downtick, because both are the same.  Let this be fixed as the realized downtick value:

By substituting for k, you can solve for the value of the put option P.

This gives you the price of the put option as a function of the current stock price, the future stock values, the strike price, and the risk-free interest rate.

For example, when X = 30, Su = 40, Sd = 20, and  one plus risk-free interest rate r = 1,

this gives S +2P = 40 so P = (40-S)/2,

An alternative approach to the European option valuation problem is to create a synthetic call option by constructing an appropriate portfolio consisting of the stock and the bond.  You can see this approach in the next topic, Option Valuation:  A Synthetic Option Approach.