n alternative way to value an option is to create a synthetic option from securities with known values.  A synthetic option is a portfolio that exactly replicates the cash flows from a real option.  If we can create a synthetic option from such securities, we can value the option, because the price of the real option must equal the price of the synthetic option.  If these prices are unequal, you would be able to make arbitrage profits by buying the cheaper one and selling the equivalent more expensive one.

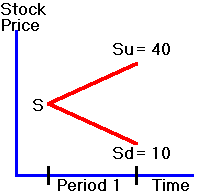
By using Option Tutor’s Binomial Replication subject, you can attempt to create the synthetic options discussed here.  To see how a synthetic option is created, consider the example where the end-of-period stock value can either be 10 or 40, and the risk-free interest rate is zero.   Figure 2.3 shows this case in a tree diagram.

Figure 2.3

Payoffs in a One-Period Environment. 

Assume a European call option with a strike price equal to 20.  In this one-period binomial world, the payoffs from this call option are:

0 if the stock price is 10,

and

20 if the stock price is 40.

Suppose the stock price, S, is 20, and you borrow $6 2/3 at the risk-free rate (which here is zero), and buy 2/3 stock at price 20.  

The total "cost" of this strategy is 6 2/3 - (2/3)S, since you get $6 2/3 borrowing and pay $40/3 for the stock.

If a downtick occurs, your stock is worth $ (2/3)10 = $6 2/3, and you will have to repay the $6 2/3 that you borrowed.  Your net position, then, is 0 if the stock price is $10.

If the stock price is 40, your stock position is worth $80/3, but you have to repay $6 2/3, leaving you with 20 if the stock price is 40.

You can see that this strategy yields exactly the same payoffs as one call option.  Simple arbitrage arguments imply that the two portfolios must cost the same (i.e., the cost of the call option must be exactly the same as the cost of the other portfolio).  If C is the price of the call,  then C = (2/3)S - $6 2/3.

Note that this approach lets us value the option without reference to any probabilities whether the stock moves up or down. 

Sometimes, if the call option is mispriced relative to the stock, you can make an arbitrage profit.  Continuing with the above example, we know that C = (2/3)S - $6 2/3.  Let Cb denote the call bid (the price that you can immediately sell a call for) and Ca be the call ask (the price that you can immediately buy a call for).  Similarly label the stock bid and stock ask, as Sb and Sa.  You can make an arbitrage profit if:

Cb  > (2/3)Sa  - $6 2/3 or if

Ca  < (2/3)Sb  - $6 2/3.

In the first case, you should sell the call and buy the synthetic call.  In the second, you should buy the call and sell the synthetic call.  Also, note that if Sb is the current stock bid, and you send to the market a call ask that satisfies the second inequality, you are providing an arbitrage opportunity for someone else!

The general one-period models for the riskless hedge and synthetic option examples are presented in topic 2.4, Call Option Valuation: A Riskless Hedge Approach, topic 2.5, Put Option Valuation:  A Riskless Hedge Approach and topic 2.6, Option Valuation: A Synthetic Option Approach.