he values of stock and option positions fluctuate because the positions are exposed to certain risks.  The value of the option depends on the value of the underlying stock, on interest rates, and so on.

The change in the value of a position with respect to a corresponding change in one of the underlying (state) variables, such as the price of underlying assets or interest rates, is referred to as the price delta, or interest rate delta of the position.

If the source of this underlying risk is tradable, the price delta tells you the number of units of the underlying security needed to hedge the risk completely.

Online, if you choose the subject Binomial Delta Hedging and reset the initial values to : stock $40, uptick 2, two-periods, call option, discrete compounding:

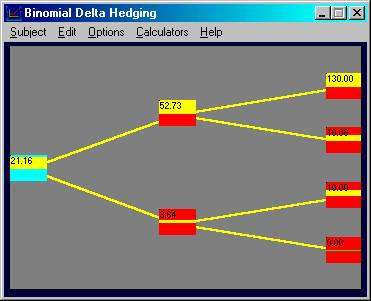
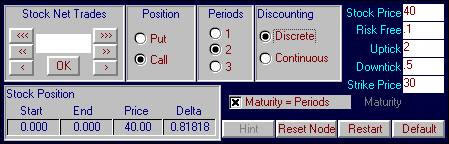
You can see in this current case that the option's delta is given to you in the Stock Positions box.  In the current example this is 0.8182.

Hedging Risk

The hedging problem is relatively straightforward when the source of the risk is the value of a tradable security, as the following example will illustrate.

Suppose you have a position in one-period call options.  The current value of one option in your portfolio is C, the value of the call.  You face risk because the value of the call in the next period will depend on what happens to the stock.  This value will either be

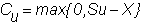
or

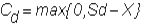
If these values are unequal, this position is exposed to stock price risk.  You may recall from the one-period option pricing model that you can form a synthetic call option from a stock and a riskless bond as follows:

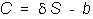
where the synthetic call consists of delta stocks plus one bond.  By rearranging this equation we can write:

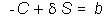
where

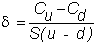
But this means that by selling delta stocks all your stock price risk has been eliminated.  In a two-period binomial model, the hedge must be adjusted at every node, since the delta can be different at every node.  We illustrate this next.

Suppose you own a two-period call option.  Consider the two nodes marked by the black dots in Figure 4.5.

Figure 4.5

Two Node Comparison

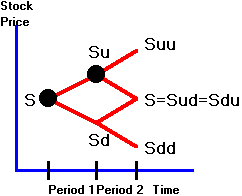
The deltas at the two nodes are generally unequal:

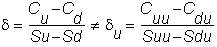
To avoid price risk, you must rebalance your portfolio at Su (and also at Sd).  The rebalancing is quite straightforward; in fact, the delta tells you what to do.  You already know that, at Su, in order to be hedged you must have:

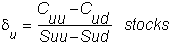
Therefore, at node Su, you must trade (du - d) stocks.  Similarly, at Sd, you must be short:

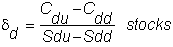
which requires a net trade of (dd -  d) stocks.

By adjusting your stock position in this manner, you can eliminate all the risk associated with the option position.  One interpretation of this argument is that you are constantly buying insurance for your initial position.  Selling stocks helps insure against a rise in the value of the option (causing a decline in the value of your short position).

Cost of Delta Hedging

So how much does this insurance cost?  Would you be better off simply selling the option and holding the riskless bond instead?

The answer is that in the absence of transaction costs and market imperfections, you must end up with exactly the risk-free return over two-periods.  Otherwise, there would be an arbitrage opportunity.  Thus, in an arbitrage-free (perfect) capital market, the insurance costs no more or no less than it should.

To check this result, recall the riskless hedge argument:  At the end of the first period, your portfolio is worth:

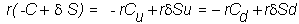
where r is the 1 plus risk-free interest rate.  By rebalancing your stock position, say, at Su, your portfolio value at the end of the second period is:

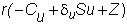
where Z is the net cash flow from rebalancing

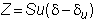
Substituting for Z, you arrive at your final position.

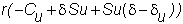
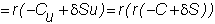
Thus, the two-period return is exactly the risk-free return over two-periods.

The same type of argument can be used to create any risk-return position desired.  For example, by buying fewer than  d stocks, we can bet on the stock price falling.

A well-known application of delta hedging is presented in the next topic, the Portfolio Insurance Problem.