4.2
The Economics of Retrading
|
W |
hat is interesting about the two-period binomial
model is that it allows determination of the option price by forming a riskless
hedged portfolio from two securities, even though we have more than two terminal
stock prices (Suu, Sud, Sdu, Sdd) and
therefore more than two distinct call option values.
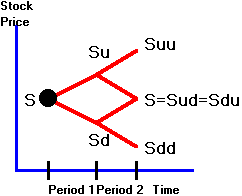
Figure
4.1
Binomial
Tree for Stock Prices
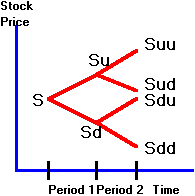
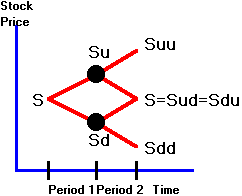
In Figure 4.1, the underlying asset value is
path-dependent whenever Sud is not equal to Sdu.
Although the same principles apply to path-dependent and path-independent
options, it is simpler to value path-independent options.
We therefore focus on them in this section.
If we assume that ud = 1, in
which case Sud = Sdu = S, then
multiple paths lead to the middle terminal node.
Figure
4.2
Binomial
Tree: Path Independent
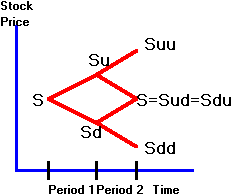
Then, after two periods, a call option with Sd
< S < X < Su has payoffs:
Suu -
X, S - X, and 0.
Now suppose you want to
form a synthetic call option from a portfolio of n stocks and m bonds.
How would you do this? Observe
that there are three possible end-of-period values to be replicated, but only
two securities to work with. The
equations you have to solve are:
nSuu
+ m Br = Suu - X
nS +
m Br = S - X
nSdd
+ m Br = 0
We have three equations and only two unknowns.
You know that one way of solving this is to create a portfolio of three
securities but you also know that you can solve for the call price from a
replicating portfolio of only two securities (the stock and the bond).
What is going on?
The answer lies in the ability to
rebalance your position. You do
not have to hold your portfolio for two periods, but instead can re-trade at the
end of the period.
You may have observed in the two-period
problem for a European call option, in Chapter 3, that the hedge ratio at
each node is different. In
particular, the three hedge ratios are:
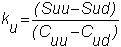
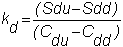
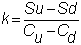
Thus, if you create
the riskless hedge portfolio at the beginning of the first period, you would
have to adjust your position at the beginning of the second period to ensure
that you have the appropriate hedge ratio.
You can apply this important principle by working
with two of Option Tutor's interactive
subjects, Binomial Replication and Binomial
Delta Hedging. The software
allows you to choose at each node the trade that should be executed either to
maintain a riskless portfolio or to create a synthetic option.
You will see that the number of stocks required to maintain a riskless
position changes at each node. You
can solve for such a position using the Binomial
Delta subject in Option Tutor.
For now, let us work backward through the tree to
try and create a synthetic option.
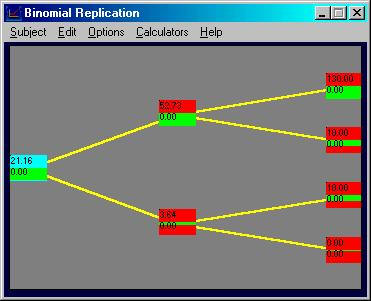
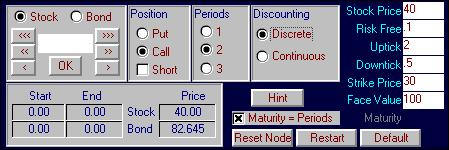
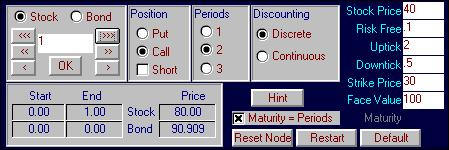
Online click on the Subject menu item and choose
Binomial Replication. Change the
default values to stock price = $40, uptick = 2, riskfree = 0.10 (discrete
compounding), strike price = 30. Similarly
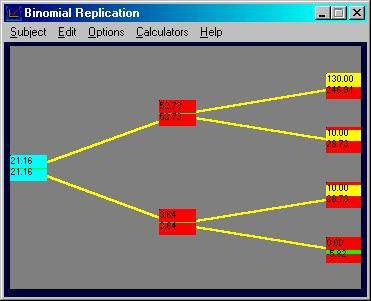
select to display the call option with a two-period life. Your screen should appear as follows:
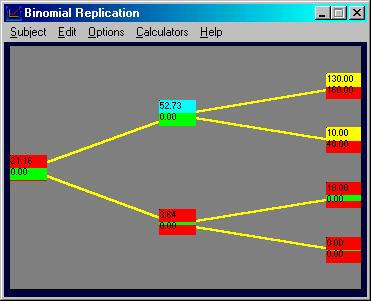
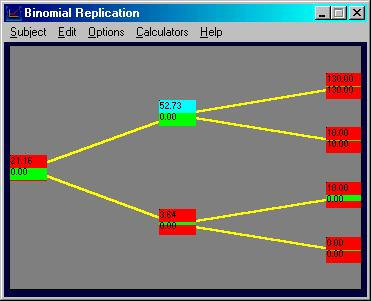
Click on the uptick node (currently labeled 52.73
and 0.00). By choosing to go long 1
stock observe that the difference between the call option payoff, and the
portfolio that has bought 1 stock (at $40), is $30.
You can see this as follows:
As a result, by introducing some riskfree bonds
result in a synthetic call option being created.
In particular consider shorting (i.e., borrowing) 0.3 riskfree bonds with
a terminal face value equal to $100. This
reduces the terminal node payoffs by $30 which results in a synthetic call
option being constructed at the first uptick node.
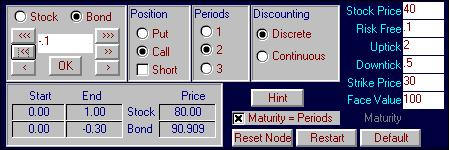
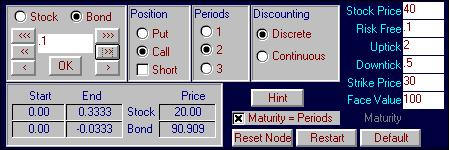
Similarly we can construct a synthetic call option
if we find that a downtick is realized resulting arriving at the node labeled
3.64. Here the stock and bond
position is 0.3333 stocks and -0.0333 bonds.
Note: to control the 0.01
digit you can click on the button with a single >. However, to control the 0.001 and 0.0001 digits to get to
four decimal place accuracy, you need to type into the box 0.001 and click OK
several times, and similarly for 0.0001. If
you want to subtract type in –0.0001 and click OK repeatedly.
After a little trial and error you will quickly control finer decimal
places.
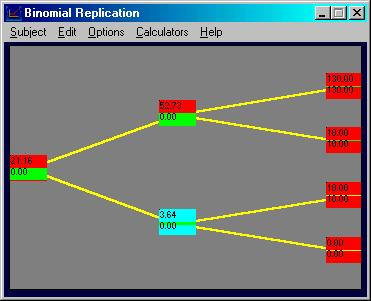
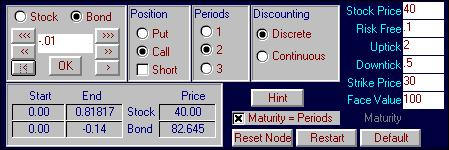
Finally, at the beginning node we can construct the
synthetic call option by first clicking on this node and then by acquiring
0.81817 stocks (using the same trick as described above to control higher
decimal places by typing in 0.00001 and clicking OK 7 times to add 0.00007) and
selling 0.14 bonds as follows:
That is, at every possible node that you can reach
there exists a position that can be constructed from stocks and bonds using
the prevailing market prices that exactly mimics the call option.
This argument is presented for the general case as
follows:
Consider the two nodes depicted as black dots in
Figure 4.3.
Figure
4.3
Binomial
Tree for Stock Values
To find the appropriate number of stocks and bonds
to create a synthetic option, let n be
the number of shares and m be the
number of risk-free bonds.
Then nu , nd , mu , md
are
node-specific and must solve:
nu Suu + mu
Br
= Suu - X
nu S + mu
Br
= S - X
nd S + md
Br
= S - X
nd Sdd + md
Br
= 0.
We now have four equations and four unknowns.
From this set of equations, you can determine the synthetic form of Cu
and Cd, as we did before.
Finally, step back to time 0, the first node.
Now there is only one node left (depicted by the black dot in Figure
4.4).
Figure
4.4
Initial
Node Reached
Again, we need to find n
and m to solve
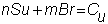
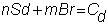
where Cu
and Cd are as obtained above.
Once you solve these equations for n
and m, you will know the price of the
call option.
The important principle here is that the ability to
trade at each node has the same effect as increasing the number of
markets that are open.
Formally, trading increases the set of possible
payoffs that we can achieve without having to open up additional markets.
Therefore, there is an interesting trade-off when hedging some risk.
The trade-off is between creating more complex portfolios as opposed to
more frequent retrading of a smaller number of securities.
Rebalancing is the essence of Delta Hedging, our next topic.
 office (412)
9679367
office (412)
9679367