13.7  Binomial Method

One way to solve for the value of an American option is to use the binomial approximation, a method attributed to Cox, Ross, and Rubinstein (1979). 

From the technical topic, Limit of the Binomial, you already know that if you make the appropriate translations of the up and down parameters and the risk-free interest rate, the binomial model converges to the Black-Scholes model. 

Here, we are simply going the other way.  We are given the risk-free rate, r, and the volatility, s.   First, decide on the number of steps in the binomial approximation (i.e., how finely we want to divide time between now and the maturity date of the option).  Let n be the number of steps.  Then, we choose the u and d parameters as follows:

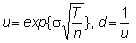
Given these parameters, we simply solve the binomial tree for the option value, checking for early exercise at every node.  Online, you can check for yourself the convergence properties of the binomial approximation to the Black-Scholes price for European options by selecting the Limit of the Binomial subject.