13.5  Finite Difference Method

The Finite Difference Method

The finite difference method is a numerical method that is used to solve the Black-Scholes partial differential equation (PDE).  We will show you the method as it applies to the American put option.

The Black-Scholes partial differential equation is

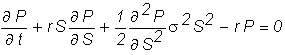
where

P = option value

r  = risk-free interest rate

s = volatility

S = stock price

t  = time

The boundary conditions for the American put  option are:

1.   P(T,S) = max{X-S,0},  where T is the expiration date of the option, and

2.   P(t,S) > max{X-S,0} for all t. 

The first condition is simply the terminal value of the put, while the second condition embodies the ability to exercise the option early.

The finite difference method solves the PDE subject to the boundary conditions using a grid.  The first and second derivatives in the PDE are approximated by taking finite differences, hence the name of the method.

The method proceeds as follows.  First, choose a maximum value for S, say S such that S > X.

Divide the interval  0 to S into m equally spaced values : S1,...,Sm, where

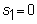
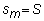
Similarly, divide time into equally spaced values:

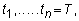
 where t1  is  today.  Let

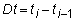
be the time difference.

Recall that the equation we have to solve is

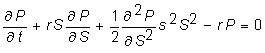
We will approximate the three terms involving derivatives. 

At point (t ,S ), approximate dP/dt by

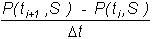
We approximate dP/dS by

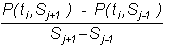
and finally, the term:

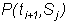
  by

If you substitute these into the PDE, you get an equation of the form

 this relates values at time t_i to those at time t_i+1, and the parameters a, b, and c only depend on stock values.

We now work backward through time.

We then know the right-hand side of the above equation for every S from the boundary conditions at maturity.  In other words, we know

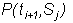
for all j.  If you look at the left-hand side of the equation, we have m equations (one for each j)  and m unknowns  (P(t i ,S) for the m different values of S).  These can be solved to obtain the values at time t i.  Now, we check each value for early exercise, and replace the calculated value of P with the exercise value if the latter is larger.  We have now solved the problem at time t i.  Continuing backwards in time, we can obtain the value of the put option at the current time.