currency option gives its owner the right to buy/sell one currency for another at a fixed exchange rate for a specified period of time.  We will adopt the convention that  an option specifies delivery of one unit of one currency in return for k units of the other. 

In practice, currency options come in both the European and American variety, although much of the volume is taken up by the American options.  Further, the actual quantities delivered depend on the currencies; we will explore this later when we look at examples of currency options.

In this topic, we derive the option pricing model for currency options.  This model, developed by Garman and Kolhagen (1983), is applied widely in practice by currency traders.

In topic 10.2, Interest Rate Parity Relationship, we referred to different currencies in terms of "strike" or "deliverable" currencies.  For example, if $U.S. is the strike currency and the Deutschmark, dm, is the deliverable currency, a currency call option gives you the right to buy 1dm for $kU.S.

If dm is the strike currency, and $U.S. is the deliverable currency, a put option gives you the right to sell  $1U.S. for k' dm.

If k'=1/k, you can immediately see that a call option (with deliverable dm) is the same as a put option (with deliverable $U.S.).

For example, options traded at the Philadelphia Stock Exchange (PHLX) have strikes in  $U.S. per one unit of deliverable currency (e.g., Australian $, British pound, Canadian $ etc.).  In each of these countries, currency options are traded with $U.S. as the deliverable currency, with the home currency being the strike currency.  If the strikes are the "same" ( i.e., k'=1/k), the call option in the U.S. should be priced exactly the same as the (equivalent) put option in the other country.

Notation

In order to develop an option pricing model for currency options, we again have to be careful with notation.  One change from before is that we use K for the strike price instead of X.

C = price of a currency call option that is defined in units of its strike currency;

P = price of a currency put option that is defined in units of its strike currency;

S = rate of exchange for one unit of deliverable currency in exchange for x units of the strike currency;

K = the strike price of the option;

T = the time left to maturity for the currency option;

s = the volatility of S;

= the risk-free interest rate for a pure discount (zero-coupon) bond with the same maturity as the currency option in the strike country;

 r_d = the risk-free interest rate for a pure discount bond with the same maturity as the currency option in the deliverable country (in practice, this is the Eurorate for the deliverable currency).

The Exchange Rate Process

The exchange rate follows the process dS = mSdt + sSdz.  Note that S is quoted as units of deliverable currency per unit of strike currency.  If you find it more intuitive, you may want to think of your domestic currency as the numerator and the foreign currency as the denominator.  For example, if your home currency is the dollar, and the foreign currency is the yen, then the exchange rate is the number of dollars per yen.  This means that if S goes up, you get more dollars per yen, and the dollar has thus depreciated.

What Makes up the Riskless Hedge

As you have seen repeatedly, the first step in valuing an option is to find a risk-free portfolio involving the option.  With a stock option, you saw that holding delta units of the stock and (plus/minus) one unit of the option gave such a portfolio. 

What do we do with an exchange rate? The problem is that you cannot “hold” the exchange rate, but only assets in the different currencies.  Therefore, the portfolio is constructed by holding risk-free bonds in the two currencies.  However, we have to be careful that when we construct this, we measure everything in the same currency.

Let Bd be the value of the bond in the deliverable currency, and Bk the value in the strike currency.  Then, the value of Bd in the strike currency is SBd, and depends on the exchange rate. 

If you find strike and deliverable currencies confusing, think of the case of an American investor interested in yen options traded on the Philadelphia Exchange.  For such an investor, the strike currency is the U.S. dollar and the deliverable currency is the yen.  Bd is a Japanese bond, and S is the number of dollars per yen. 

The riskless portfolio is constructed by holding Bd and the option, and measuring everything in the strike currency.  In units of the strike currency, the two assets are SBd and C.

The Option Pricing Formula

It turns out that the formula for the currency call option is the same as that for an option on a stock paying a continuous dividend yield (see Chapter 9, topic 9.2) where the yield is rd.  This is quite intuitive if you think of the asset SBd.  This asset has a drift rate equal to m + rd, which is the depreciation/appreciation of the exchange rate plus the return on the bond.  The formal equivalence of this is derived in Chapter 12, topic 12.4, Application:  Currency Options.

The Garman-Kolhagen European call option price is:

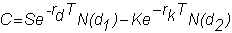
and since log(S'/K) = log(S/K) - rdT

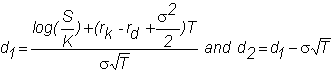
The European put option price is:

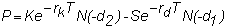
where d1 and d2 are as before.

Example

Consider the following information for options on the US Dollar and British Pound.  The spot exchange rate is 1.73 (dollars per pound).  The 3-month risk-free interest rate in the US is 5%, while that in Britain is 6.45%.  The volatility of the exchange rate is estimated to be 0.15.  Then, the value of a call option with strike price 1.7 is just over 6 cents (0.0629).  The value of a put option with the same strike is 4 cents.

As before, a major feature of the currency option pricing model is that it provides traders with an analytical description of the hedge parameters.  These parameters are discussed in topic 10.4, Currency Options:  Hedge Parameters.