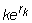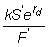s a prelude to valuing currency options, we show you an arbitrage relationship that must hold between spot and forward exchange rates.  This will help you understand how a riskless hedged portfolio is constructed, by identifying the various opportunity costs involved in dealing with currencies.

In a forward contract, two parties enter into an agreement to exchange one asset for another.  Unlike an option, the exchange must be carried out.  The price is specified now, as is the date at which the transaction will occur.  This type of contract is very popular for currency transactions.  The price that is set now is called the forward exchange rate.  This rate will govern the future exchange, no matter what the spot exchange rate is in the future.

The existence of a forward exchange market enables the construction of a riskless portfolio.    As you will see, this implies that certain relationships must hold among the spot exchange rate, the forward exchange rate, and interest rates in the two countries.

These relationships are summarized by the interest rate parity theorem.  This theorem also tells you how to value a forward contract.

We start with some notation.  Understanding the notation is particularly important when dealing with currencies.  To maintain consistency (particularly when we come to options), we adopt a convention for referencing a country's currency relative to the  option contract:  One country's currency is labeled the "strike currency." The other country's currency is labeled the "deliverable currency." 

Notation:

F = the forward exchange rate.  This is the number of units of the strike currency to be exchanged for one unit of the deliverable currency.  We set the maturity of the forward contract to be one period.

S = the spot exchange rate.   This is the number of units of the strike currency that can be exchanged  for one unit of deliverable currency at the present time.

F' and S' are the same as F and S, with strike and deliverable currency interchanged.

 r_d = one-period continuously compounded risk-free rate for the deliverable currency.

   r_k = one-period continuously compounded risk-free rate for the strike currency.

Interest Rate Parity Theorem

Suppose you have k units of the strike currency to invest for one period.  You are  interested in the final value of the strike currency.  If you consider only risk-free investments, there are two ways in which you could invest the money.

1.  At the strike currency's risk-free rate.

2. At the deliverable currency's risk-free rate, where you go through three steps:

a.  Convert k at the spot exchange rate into the deliverable currency.

This gives you kS' of the deliverable currency. (Recall that S' is the number of units of the deliverable currency per unit of the strike currency.)

b.  Invest at the risk-free rate in the deliverable currency.

At the end of the period, you have

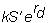
of the deliverable currency.

c.  Eliminate all risk by entering into a forward agreement to buy back the strike currency at the forward exchange rate.

This nets you the result in b) divided by F' (which again is in the same units as S').

The payoffs from the first and second strategies are:

Table 10.1

Risk-Free Investments:  Two Strategies 

Neither strategy entails any risk.  Therefore, the two strategies must have the same future (or present) values.  This implies

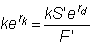
Rearrangement gives us the  interest rate parity theorem:

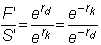
Alternatively, observe that:

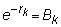
price of a one-period pure discount bond with face value 1, and, similarly,

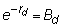
Again, substituting and rearranging yields:

If the period length is some number T, the parity relationship is:

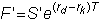
In terms of the strike currency, the relationship is

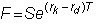
The parity relationship says that  spot and forward exchange rates should be such that a trader cannot engage in profitable arbitrage.  That is, a currency trader should not be able to borrow cash in one country, convert it at the spot exchange rate, invest in the second country, and at the same time enter into a (zero cash outlay) forward agreement to cover the future value of the loans, and have some positive amount of cash left over!

Now that you are acquainted with this important relationship, you are ready to move on to the  Currency Option Pricing Model.