3.3 Spot Rates and the Yield to Maturity

13.3 Applications: Currency Forwards and Futures

ere we show how to calculate the prices of currency options. To provide relevant background material we first derive the prices of currency forwards and futures. This gives some useful insight into the appropriate interest rates to use from the two countries for valuing options. You will value options on different currencies that are traded at both the Chicago and Philadelphia exchanges. This exercise demonstrates how the theory is applied and what problems arise in applying the theory.

Table 13.7 gives closing prices for currency and currency forward contracts for the British pound, the yen, and the Deutschmark on March 30, 1994 (Source: The Wall Street Journal).

Table 13.7

Currency Closing Price Data

Country

U.S.$ Equivalent

Currency per U.S.$

Britain (Pound)

1.4800

0.6757

30-Day Forward

1.4781

0.6765

90-Day Forward

1.4747

0.6781

180-Day Forward

1.4714

0.6796

Germany (Mark)

0.5968

1.6755

30-Day Forward

0.5958

1.6785

90-Day Forward

0.5941

1.6832

180-Day Forward

0.5926

1.6874

Japan (Yen)

0.009713

102.95

30-Day Forward

0.009725

102.83

90-Day Forward

0.009753

102.53

180-Day Forward

0.009807

101.97

Currency Forwards

The majority of foreign currency transactions, other than spot exchanges, occur as forward contracts. A forward contract is a contract entered into between two parties (generally banks dealing with other banks) that obligates each party to exchange one currency for another at a specified future time and at a price fixed today.

There is no organized secondary market for forward contracts. Unlike futures contracts, they are not marked to market on a daily basis.

To value the forward contract we will use the London Inter Bank Offered Rate (LIBOR) shown in Table 13.8. This is the rate for time deposits of funds in major banks that are outside the funds' country of origin. LIBOR is quoted on an annualized basis using a 360-day year.

Table 13.8

LIBOR

Country

1-month

2-month

3-month

6-month

12-month

Britain

5.17709

5.32292

5.39584

5.54167

5.79167

Germany

5.78572

5.75000

5.70536

5.62500

5.46429

Japan

2.31250

2.43750

U.S.

3.68750

3.81250

3.93750

4.25000

4.75000

Source: FAST Trading Room, Carnegie Mellon University

The Interest Rate Parity RelationshipIRPR_CO (see Chapter 10, topic 10.2), describes the arbitrage-free relationship between spot and forward exchange rates. This relationship is:

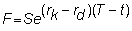
where r_d is the interest rate that is applicable to the deliverable currency in the forward contract, and is the interest rate that is applicable to the currency received in exchange (in option parlance this is the strike currency), and S is the spot exchange rate.

From Tables 13.7 and 13.8 you can observe that the one-month forward on the German mark is U.S.$ 0.5958. The LIBOR for the one-month U.S.$ is 3.6875%, and for the German mark is 5.78572%. As a result, the forward exchange rate predicted from the interest rate parity theorem is:

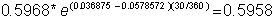
Similarly, by applying the above formula using the appropriate LIBOR rates, you can verify that the predicted 90-day and 180-day forward rates are 0.5942 and 0.5928, respectively, which compare very well with the quoted rates.

You can check out the fit between predicted and actual forward prices for other currencies using the LIBOR table.

Currency Futures

The major difference between currency forwards and futures is that futures is a standardized contract traded on organized exchanges and marked to market at the end of each day. You saw that the forward valuation model applies to a futures contract if interest rates are not stochastic. Casual empiricism does not support this assumption, but we can see how well the interest rate parity theorem performs when applied to futures prices.

For the same date (March 30, 1994) as above, the closing futures prices quoted in The Wall Street Journal are as given in Table 13.9.

Table 13.9

Closing Futures Prices

Country

June

September

December

March 95

Britain

1.4758

1.4718

Germany

0.5948

0.5930

0.5923

0.5924

Japan

0.9758

0.9813

0.9872

Delivery Day

June 15

Sept 21

Dec 21

Mar 15

The delivery day for foreign currency futures is the third Wednesday of the contract month.

In the case of the March, 1995 future on the German mark, you can verify that forward and futures prices are pretty much equal. The predicted price is 0.5926 compared to the actual price of 0.5924. For other cases, you can either use the closest LIBOR or interpolate from the LIBOR term structure of interest rates.

For example, for the September futures suppose we use the six-month LIBOR. We would get the values shown in Table 13.10.

Table 13.10

Predicted Futures Prices as Forward Prices

Country

6-Month LIBOR

Futures

Predicted

Britain

5.54167

1.4718

1.4705

Germany

5.625

0.5930

0.5927

Japan

2.3125

0.9813

0.9807

U.S.

4.25

Again, when we use the LIBOR data, the futures prices are well approximated by the forward price (i.e., the constant interest model for futures prices).