9.3  Comparative Statics

n important application of option pricing models is to manage risk.   The option pricing model identifies the value of the option as a function of different variables such as the underlying asset’s price and volatility.  Therefore, the change in the option’s value that results from a small change in valuation variable can be calculated.  Recall from Chapter 7 that this number, referred to as a comparative static, is used to identify portfolios that can hedge risk.

The comparative statics derived in this section allow the comparative statics of any application of this continuous constant dividend yield model to be derived by using an appropriate substitution for q, the constant continuous dividend yield.

The call option pricing formula for the constant dividend yield model is

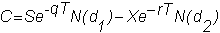
and since ln(S'/X) = ln(S/X) - qT

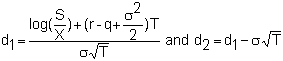
The underlying variables that determine the option's value are as before, except for the addition of a constant dividend yield term, q:

S =  the stock price

r   = the interest rate

q  = constant continuous dividend yield

s  = the volatility

X  = the strike price

T  = the time to maturity

Once again, the partial derivative of the call price with respect to each variable is computed.  This characterizes the effect of a small change in the variable on the value of the call, holding all other variables constant.

Delta

The derivative of an option with respect to the underlying stock price is called the delta of the option.  It provides a measure of the price risk associated with a particular position.

For a call option and a put option,  respectively, it is given by

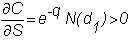
and

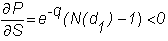
Delta tells us how the value of the call will change if there is a small change in the price of the underlying stock. 

Gamma

The gamma of an option measures how the delta changes with S.  This is useful in that, in theory, delta hedging requires continual rebalancing.  This of course is impossible to implement and even very frequent rebalancing would be prohibitively expensive.  The gamma tells you how far you are from a hedged position.  It is given for a call option by

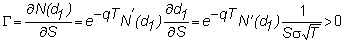
Online, in the Option Sensitivities subject, you can see that a position is most sensitive to changes in delta when it is "at-the-money."  That is, the strike and underlying asset price are about the same.

Vega (Lambda or Kappa)

The vega measures the effect of a change in the volatility of the underlying stock.  It is also known as lambda and kappa.  It is given by

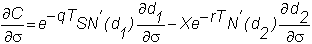
and thus

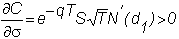
Suppose you hold a position that is delta-gamma-hedged.  This position is not hedged against shifts in the underlying security's volatility.  As a result, a trader holding a delta-neutral position is effectively betting on a volatility shift.  If volatility increases, then from the comparative statics analysis, the value of the option is expected to increase.  On the other hand, if volatility declines, then the option value will fall.

Again, if you want to be delta-, gamma-, and vega-hedged for small changes, this requires at least  three securities.

Rho

Rho measures the change in the call option with respect to a change in the risk-free interest rate.  It is given by

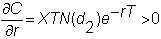
Theta

Theta measures the change in the call option with respect to a change in time.  This is  useful for understanding the behavior of  option prices over time.  It is given by

Strike Price

The change in the call option with respect to a change in the strike price is not a risk that we are interested in hedging, but again it is useful for understanding the behavior of an option price over different contractual specifications.  It is given by

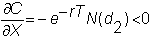
In this topic, we have reviewed the basic set of option sensitivities with respect to  small changes in the underlying pricing variables.  Next we focus our attention on some important applications of the continuous dividend yield model.  The first application is valuing Currency Options,  which is presented in Chapter 10.