ecall that the call option pricing formula is

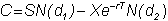
where

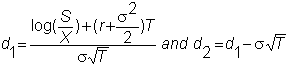
The variables that determine the option's value are:

S    the stock price

r     the interest rate

s    the volatility

X    the strike price

T    the time to maturity

To calculate how the variable affects the option price, we simply take the derivative of the call price with respect to that variable.  These derivatives are called the hedge parameters, and measure the sensitivity of the option price to the variable. This sensitivity tells you how the option value changes with a small change in the variable.  If you view these variables as risky, then this is called your (local) exposure to the variable.

There are several limitations to this analysis. 

First, the sensitivity you obtain is relevant only for small changes in the variable, and can be quite misleading if there is a large change. 

Second, if you use this model to hedge a position, you should understand that the numbers you get are only as good as the option pricing model.  If the Black-Scholes model is an accurate model of real-world option prices, the numbers will serve you well;    otherwise, they will not.

Third, you should recognize that the model assumes that the stock price evolves continuously.  This means that the option price also evolves continuously, and therefore so do the hedge parameters.

Finally, note that even though we are going to measure the sensitivity to, say, the risk-free interest rate, the model actually assumes that the interest rate is constant.  The same applies to volatility.  In spite of this limitation, the Black-Scholes hedge parameters are widely applied to measure and hedge the risk from these factors.

Because the hedge parameters are denoted by Greek letters they are sometimes called the "option Greeks."

Delta

The partial derivative of the option value with respect to the underlying stock price is called the delta of the option. 

For a call option it is given by

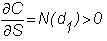
and for a put option it is given by

 .

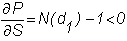
Thus, N(d1) is the delta of the call; it tells us how the value of the call will change if there is a small change in the underlying stock price. 

The formal derivation of delta is provided in the technical topic 7.3, Derivation of Delta.

To show how the delta is used to hedge the risk of stock price changes, suppose you own one call option.  You want to ensure that a small change in the stock price does not affect the value of your call position.  One way to do this is to sell delta (D) stocks. If you do this, your position is

-D stocks, +1 call

and the value of the position is

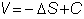
Then,

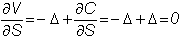
Now, you are completely hedged against price risk.  Of course, this would not be true if there were a large change in the stock price.  Note also that over time, you would have to hedge your position continuously to maintain the initial value.  This is called "rebalancing."   You may see the similarities with the delta hedging that you studied for the binomial model in Chapter 4, topic 4.3.

For example, suppose that you have written (or sold) 1,000 call options, and the delta of each option is 0.7.  Then, you would need to be long 700 stocks to be hedged, or to be "delta neutral."  If the delta changes to 0.71, you would need to purchase an additional 10 stocks to maintain neutrality.  The phrase, "delta-neutral," means that the delta of your position (i.e., the options and the stocks) is zero.

More generally, the delta of your position measures the exposure of your position to price risk.  In layman's terms, it measures the "bet" that you have taken that prices will rise or fall.   For example, consider the portfolio:

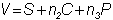
The position delta is:

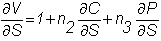
If this is positive, say, it equals 1,000, then every $1 increase in S translates into a  $1,000 increase in the value of your position.  With this position, you have taken a bet that the stock price will rise.  Of course, you lose $1,000 if the stock price falls by a dollar! 

Similarly, a negative delta is a bet that the stock price will fall.

Gamma

The gamma of an option measures how the delta changes with S.  This is useful in that  delta hedging requires continual rebalancing of your portfolio.  The transaction costs associated with trade make it prohibitively expensive to trade so frequently.  If you re-balance less frequently than required, you need to know how far you are from a hedged position.

The gamma tells you how far you are from a hedged position.  For both put and call options, gamma is given by

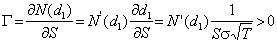
Online, in the subject Option Sensitivities, you can see that an option is most sensitive to changes in delta when it is "at the money" (i.e., the strike and underlying asset price are about the same).  You will also see that this sensitivity increases as the option gets closer to maturity.

Suppose you want your call option position to be both delta- and gamma-hedged against small changes in the stock price.  You cannot do this with just the stock, as we did before.  Instead you need at least two securities (e.g., a stock and, say, a put option).

To see this, suppose that you have written (sold) n2 call options, but wish to maintain a position that is both delta- and gamma-neutral.  Your position delta is:

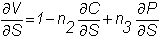
and the position gamma is:

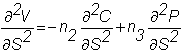
You have to choose n2 and n3 to make the left-hand side of both equations zero.  You can do this since you have two equations and two unknowns.  This also shows you why you need two securities to create a delta- and gamma-neutral position for your option  writing activities.

Vega (Lambda or Kappa)

The vega measures the effect of a change in the volatility of the underlying stock.  It is also known as lambda and kappa.  The vega is the same for puts and calls.  The calculation for a call is

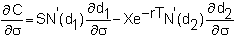
and thus 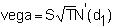 > 0

Suppose you hold a delta-neutral position where you are long one call and short delta stocks. This position is not hedged against shifts in the stock's volatility; the vega of the position equals the vega of the call, and is positive.  As a result, a trader holding a delta-neutral position is effectively betting on a volatility shift.  If volatility increases, then the value of the position is expected to increase.  On the other hand, if volatility declines then the position value will fall.

If you desire to be delta-, gamma-, and vega-hedged, then you need at least three securities in addition to your existing position.  In hedging volatility risk using vega, you need to remember that in the option pricing model, volatility was assumed to be constant over the life of the option.

Also note that the sign of vega is positive.  This implies that options defined on more volatile stocks are more valuable than options defined on less volatile ones.  You might like to recall the example we considered when applying the certainty model to pricing IBM American call options in Chapter 6, topic 6.2, Option Valuation under Certainty.   In this example, the certainty model systematically underpriced the call option.  This is consistent with the Black-Scholes model, since volatility was ignored.

Rho

Rho measures the change in the option price with respect to a change in the riskless interest rate.  For a call option, rho is

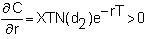
For a put option, rho is

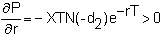
Theta

Theta measures the change in an option price with respect to the option's maturity.  This is not a "risk" that we are interested in hedging, but it is useful for understanding the behavior of an option over time.  For a call option, theta is

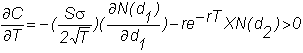
For a put option, the theta is

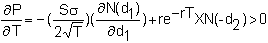
Strike Price

Finally, for completeness, we show you how the option price changes with the strike price.  For a call option, the partial derivative with respect to the strike price is:

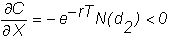
For a put option, the strike price is:

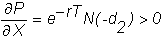
This completes our discussion of the comparative statics of the Black-Scholes model.  In the next chapter we look at some common option trading strategies.  The Black-Scholes model lets you value calendar spreads at a future point in time.  Chapter 9 presents an important extension of the Black-Scholes model which is to relax the assumption that the stock pays no dividends.  This extension is important for virtually every practical application of the model.  In Chapter 9, topic 9.2, Constant Continuous Dividend Yield Option Pricing Model, the pricing model is extended to the case where the stock pays a continuous constant dividend yield.  Later you will see, this simple extension lets you apply the model not only to such stocks, but also to futures, currencies, and stock indices.