ou learned about forward contracts in Chapter 10, in topic 10.2, Interest Rate Parity Relationship.  In a forward contract, two parties enter into an obligation to exchange one asset for another at a price specified now but paid at a fixed time in the future.  No cash is exchanged at the time of buying or selling a forward contract.  Therefore, to avoid arbitrage, the forward price must be set so that the net present value of the contract is zero.

You can see how the arbitrage-free forward price is determined if you consider the following two alternatives.  In alternative A you buy a forward contract at time 0, and at T in the future you receive the asset and pay $F cash.  In alternative B you purchase the asset today for $S (its price today) by borrowing $S cash for time period T at the risk-free interest rate r.  At time T you repay the loan.

In either case, you do not need any of your own money today.  At time T, your position under alternative A is:

-$F cash, +1 unit of the asset

while under alternative B, it is:

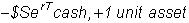
In either case, you have the asset at time T.  Therefore, the two alternative ways of buying the asset must cost the same.  Otherwise, you can make arbitrage profits.  This means:

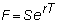
A variation on this is that it costs you something to hold the asset until period T.  This cost is called a “carrying cost.”  For example, if the asset is a commodity, such as wheat, you will generally have to pay to store the commodity.  Such costs are easily accommodated.  Suppose you pay a lump sum at time T; then, we must have

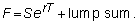
If you have to pay the cost “continuously,” say, at rate b, then we must have

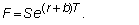
To see why this relationship must hold, suppose that the forward price F is strictly greater than SerT (a similar argument applies if it is strictly less).

In this case, you would want to sell the forward contract for $F, borrow $S for time T, and buy the asset at the current spot price.  By the nature of a forward contract, you will not receive any cash now for this transaction, and we will assume that holding costs are zero.  At the end of the contract's life, however, you must deliver one unit of S for the forward price $F.  Thus, at this time you deliver your one unit of S, receive $F, and repay the loan.

This chain of transactions leaves you with

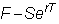
cash in hand, which by our original assumption is strictly positive.

In Chapter 10, topic 10.2, Interest Rate Parity Relationship, the general form for the arbitrage-free valuation of a currency forward contract is derived as an extension of this model to accommodate the interest rates for each currency:

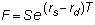
Futures Contracts

The primary difference between a futures contract and a forward contract, from a valuation perspective, is that the futures contract is marked to market on a daily basis.  What this means is that the futures price is reset so that the value of the futures contract is zero.  All outstanding contracts are then adjusted by adding or subtracting cash from the accounts of the contract holders.

For example, suppose you sold one futures contract at the futures price F and subsequently the spot price, S, rises to S '.  Your futures contract is now worth a negative amount.  To see why, let F ' be the new forward price (the future value of the spot price assuming carrying costs are zero):

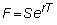
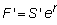
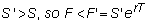
When your contract is marked, your account has the difference

Similarly, if you make money, your account has the difference added to it.

If interest rates are stochastic, it is not so easy to value futures contracts (or options on futures).  This is because the arbitrage argument outlined in the previous section no longer applies; alternative A may cost you more or less than alternative B, depending on the path of interest rates.

In practice, a commonly made assumption is that for the purposes of valuing futures and options on futures, interest rates can be taken to be deterministic.  It turns out that in this case, forward and futures prices must be the same, and we can value options on forwards and futures in the same way.  The argument is due to Cox, Ingersoll, and Ross (1981), and we show you a two-day version of their argument when the interest rate is constant.

Assume delivery takes place on day 2.  Let F0 be the current futures price, and let F1  and F2 be the futures prices at the end of days 1 and 2.  The futures strategy is to buy er futures contracts at the end of day 0 and to buy the same number again at the end of day 1. Consider what marking to market does. 

 .

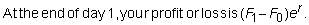
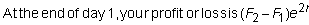The future value of these additions/subtractions (at the end of day 2) is

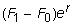
compounded once plus

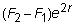
which comes out to

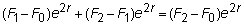
But F2 is the futures price at time of delivery, and must equal the spot price on day 2, S2, so the net result is

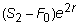
Now, suppose you buy e^2r forward contracts at the forward price, say G0.  At time 2, you would receive the asset, worth S2, and would pay G0 for each contract, yielding you a value of

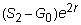
If F0 > G0, you can pursue the following arbitrage strategy: sell the first strategy (i.e., go short the sequence of futures trades) and buy the second strategy (i.e., go long the forwards).  You will make money no matter what S2 turns out to be.

The argument can be extended to cover the case where interest rates follow a deterministic path; you simply adjust the number of contracts you buy to make the end result the same.

Like many others, we assume that for the purposes of valuing futures contracts, interest rates can be taken to be deterministic.  This allows us to value not only futures contracts but also options on futures (or forwards).  This model was first developed by Black (1976).  Online, click on the Pricing of Options on Futures to see Black's options on futures pricing model.